Trong bài viết Lý thuyết toán cơ bản trong Deep Learning, ta đã biết rằng mạng nơ-ron hoàn toàn bao gồm chuỗi các phép toán tensor, và những phép toán tensor này chỉ là các biến đổi hình học đơn giản của dữ liệu đầu vào. Do đó, ta có thể hiểu một mạng nơ-ron như là một biến đổi hình học rất phức tạp trong một không gian đa chiều, được thực hiện thông qua một loạt các bước đơn giản.
Trong không gian 3D, hãy tưởng tượng hai tờ giấy màu: một màu đỏ và một màu xanh. Đặt một tờ lên trên tờ kia. Bây giờ nắm gọn chúng lại thành một quả cầu nhỏ. Quả cầu giấy bị nhàu nát đó chính là dữ liệu đầu vào của bạn, và mỗi tờ giấy là một lớp dữ liệu trong một vấn đề phân loại. Mục đích của mạng nơ-ron là tìm ra một phép biến đổi của quả cầu giấy để làm cho hai lớp trở nên có thể phân biệt rõ ràng hơn.
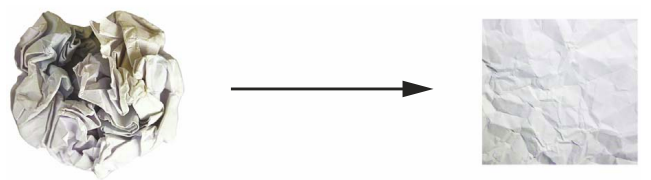
Trong học sâu, điều này sẽ được thực hiện dưới dạng một loạt các biến đổi đơn giản của không gian 3D.
Việc làm phẳng quả cầu giấy chính là nội dung của máy học: tìm kiếm các biểu diễn gọn gàng cho các tập dữ liệu phức tạp, có nhiều gập khúc, trong các không gian có số chiều cao (một “manifold” là một bề mặt liên tục, giống như tờ giấy nhàu nát của chúng ta). Tại điểm này, học sâu tiếp cận việc phân rã một biến đổi hình học phức tạp thành một chuỗi dài các biến đổi cơ bản, đó chính là chiến lược mà một con người sẽ theo để làm phẳng một quả cầu giấy.
Tối ưu hóa dựa trên độ dốc (Gradient-based Optimization)
Giả sử mỗi tầng nơ-ron của một mô hình học sâu biến đổi dữ liệu đầu vào như sau:
output = relu(dot(input, W) + b)
Trong biểu thức này, W và b là các tensor là thuộc tính của layer. Chúng được gọi là trọng số hoặc các tham số có thể đào tạo của layer (tương ứng là các thuộc tính kernel và bias). Những trọng số này chứa thông tin mà mô hình học được từ việc tiếp xúc với dữ liệu huấn luyện.
Ban đầu, ma trận trọng số này được điền với các giá trị ngẫu nhiên nhỏ (một bước được gọi là khởi tạo ngẫu nhiên). Đó là một điểm xuất phát. Sau đó, bước tiếp theo là điều chỉnh từng bộ trọng số này dần dần, dựa trên một tín hiệu phản hồi. Sự điều chỉnh dần dần này, còn được gọi là quá trình huấn luyện, là điều mà học máy đang nói đến.
Quá trình này diễn ra trong vòng lặp huấn luyện (training loop), hoạt động bằng cách lặp lại các bước nào đó trong một vòng lặp, cho đến khi giá trị mất mát đạt đến mức đủ thấp.
- Vẽ một lô (batch) mẫu huấn luyện, x, và các mục tiêu tương ứng, y_true.
- Chạy mô hình trên x (một bước được gọi là chuyển tiếp – forwarding) để có được dự đoán, y_pred.
- Tính toán mất mát của mô hình trên batch, là mức độ chênh lệch giữa y_pred và y_true.
- Cập nhật tất cả trọng số của mô hình một cách giảm nhẹ mất mát trên batch này.
Bước 1 chỉ là input/output của mô hình. Bước 2 và 3 chỉ là việc áp dụng một số phép toán tensor. Phần khó khăn nhất là bước 4: cập nhật trọng số của mô hình. Cho một hệ số trọng số mô hình, làm thế nào ta có thể tính toán xem hệ số đó nên tăng hay giảm?
Một giải đơn giản nhất có thể là đóng băng tất cả các trọng số trong mô hình ngoại trừ hệ số skalar đang xem xét và thử nghiệm các giá trị khác nhau cho hệ số này. Giả sử giá trị ban đầu của hệ số là 0.3. Sau qua trình forwarding trên một lô dữ liệu, mất mát của mô hình trên lô là 0.5. Nếu bạn thay đổi giá trị của hệ số thành 0.35 và chạy lại qua trình chuyển tiếp, mất mát tăng lên thành 0.6. Nhưng nếu ta giảm hệ số xuống 0.25, mất mát giảm xuống 0.4. Trong trường hợp này, có vẻ như việc cập nhật hệ số bằng -0.05 sẽ góp phần giảm thiểu mất mát. Điều này sẽ phải được lặp lại cho tất cả các hệ số trong mô hình.
Nhưng cách tiếp cận như vậy sẽ làm cho hiệu suất trở nên kinh khủng vì ta sẽ cần tính toán hai qua trình chuyển tiếp (rất tốn kém) cho mỗi hệ số (thường là hàng nghìn và đôi khi lên đến hàng triệu). may mắn thay, có một cách tiếp cận tốt hơn nhiều: gradient descent.
Gradient descent là kỹ thuật tối ưu hóa độ mạnh mẽ cho các mạng nơ-ron hiện đại. Nếu nhìn vào z = x + y, ví dụ, một sự thay đổi nhỏ trong y chỉ dẫn đến một sự thay đổi nhỏ trong z, và nếu ta biết hướng thay đổi của y, ta có thể suy luận hướng thay đổi của z. Trong toán học, người ta gọi những hàm này này là những hàm có thể đạo hàm được. Điều này giúp ta sử dụng một toán tử toán học gọi là độ dốc để mô tả cách mất mát thay đổi khi di chuyển các hệ số của mô hình theo các hướng khác nhau. Nếu tính toán được độ dốc này, ta có thể sử dụng nó để di chuyển các hệ số (tất cả cùng một lúc trong một bước cập nhật, thay vì từng cái một) theo một hướng giảm mất mát.
Đạo hàm là gì?
Chắc hẳn ai cũng đã học về đạo hàm ở lớp 11, xét hàm số liên tục f(x) = y, ánh xạ một số x thành một số mới y.
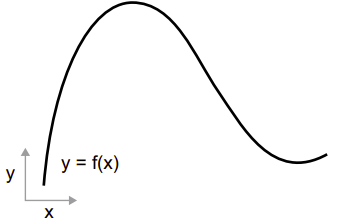
Bởi vì hàm số là liên tục, một sự thay đổi nhỏ trong x chỉ có thể dẫn đến một sự thay đổi nhỏ trong y. Giả sử tăng giá trị x một lượng nhỏ là epsilon_x, điều này dẫn đến một sự thay đổi epsilon_y nhỏ đối với y, như được thể hiện trong hình bên dưới:
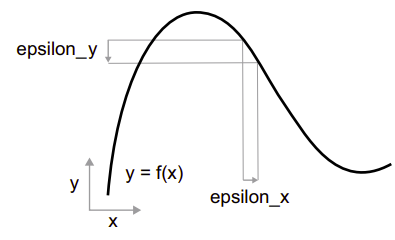
Ngoài ra, do hàm mềm mại (đường cong của nó không có bất kỳ góc đột ngột nào), khi epsilon_x đủ nhỏ, xung quanh một điểm p nào đó, có thể xấp xỉ f như là một hàm tuyến tính với độ dốc a, sao cho epsilon_y trở thành a * epsilon_x:
f(x + epsilon_x) = y + a * epsilon_x Rõ ràng, xấp xỉ tuyến tính này chỉ có hiệu lực khi x đủ gần với p. Độ dốc a được gọi là đạo hàm của f tại p. Nếu a là âm, có nghĩa là một sự tăng nhỏ về x xung quanh p sẽ dẫn đến f(x) giảm, và nếu a là dương, x tăng sẽ dẫn đến f(x) tăng. Hơn nữa, giá trị tuyệt đối của a (độ lớn của đạo hàm) cho ta biết mức độ tăng hoặc giảm này sẽ diễn ra nhanh chóng như thế nào.
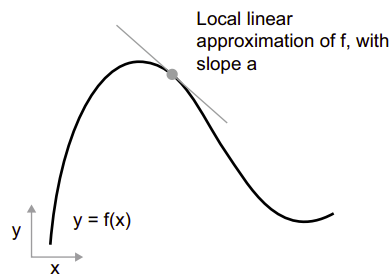
Đối với mọi hàm f(x) có thể đạo hàm, tồn tại một hàm đạo hàm f'(x), ánh xạ giá trị của x đến độ dốc của xấp xỉ tuyến tính cục bộ của f tại những điểm đó. Ví dụ, đạo hàm của cos(x) là -sin(x), đạo hàm của f(x) = a * x là f'(x) = a, và cứ thế. Việc có khả năng rút gọn các hàm là một công cụ rất mạnh mẽ khi nói đến tối ưu hóa, nhiệm vụ là tìm giá trị của x để giảm thiểu giá trị của f(x). Nếu bạn đang cố gắng cập nhật x bằng một hệ số epsilon_x để giảm thiểu f(x), và bạn biết đạo hàm của f, thì đạo hàm hoàn toàn mô tả cách f(x) thay đổi khi ta thay đổi x. Nếu bạn muốn giảm giá trị của f(x), bạn chỉ cần di chuyển x một chút theo hướng ngược lại với đạo hàm.
Đạo hàm của một phép toán tensor: Độ dốc
Hàm mà ta vừa xem xét chuyển một giá trị scalar x thành một giá trị scalar khác y: ta có thể biểu diễn nó như là một đường cong trên một mặt phẳng 2D. Bây giờ hãy tưởng tượng một hàm chuyển một bộ dữ liệu của các giá trị scalar (x, y) thành một giá trị scalar z: đó sẽ là một phép toán vector. Ta có thể biểu diễn nó như một bề mặt 2D trong không gian 3D (được index bởi các tọa độ x, y, z). Khái niệm của việc lấy đạo hàm có thể được áp dụng cho bất kỳ hàm nào như vậy, miễn là các bề mặt mà chúng mô tả liên tục và mềm mại.
Đạo hàm của một phép toán tensor (hoặc hàm tensor) được gọi là độ dốc (gradient). Độ dốc chỉ là sự tổng quát hóa của khái niệm đạo hàm cho các hàm nhận tensors làm đầu vào. Đối với một hàm scalar, đạo hàm biểu thị độ dốc cục bộ của đường cong của hàm? Tương tự, độ dốc của một hàm tensor biểu thị sự cong của bề mặt đa chiều được mô tả bởi hàm. Nó mô tả cách đầu ra của hàm thay đổi khi các tham số đầu vào thay đổi.
Xét một ví dụ liên quan đến máy học. Giả sử:
- Một vector đầu vào, x (một mẫu trong bộ dữ liệu)
- Một ma trận, W (các trọng số của một mô hình)
- Một mục tiêu, y_true (điều mà mô hình nên học để liên kết với x)
- Một hàm mất mát, loss (được thiết kế để đo lường khoảng cách giữa dự đoán hiện tại của mô hình và y_true)
Ta có thể sử dụng ma trận W để tính toán một dự đoán mục tiêu y_pred, sau đó tính toán mất mát hoặc không khớp giữa dự đoán mục tiêu y_pred và mục tiêu y_true.
y_pred = dot(W, x)
loss_value = loss(y_pred, y_true) Bây giờ chúng ta muốn sử dụng độ dốc để tìm cách cập nhật W để giảm giá trị mất mát. Làm thế nào chúng ta có thể thực hiện điều này?
Với các đầu vào cố định x và y_true, các phép toán trước đó có thể được hiểu là một hàm ánh xạ giá trị của W (các trọng số của mô hình) đến giá trị mất mát.
loss_value = f(W) Giả sử giá trị hiện tại của W là W0. Sau đó, đạo hàm của f tại điểm W0 là một tensor grad(loss_value, W0), có cùng shape như W, trong đó mỗi hệ số grad(loss_value, W0)[i, j] chỉ ra hướng và độ lớn của sự thay đổi trong loss_value khi bạn thay đổi W0[i, j]. Tensor đó grad(loss_value, W0) là độ dốc của hàm f(W) = loss_value tại W0, cũng được gọi là “độ dốc của loss_value theo W xung quanh W0.”
Vậy grad(loss_value, W0) đại diện cho gì? Các bạn đã thấy trước đó rằng đạo hàm của một hàm f(x) của một hệ số đơn có thể được hiểu là độ dốc của đường cong của f. Tương tự, grad(loss_value, W0) có thể được hiểu là tensor mô tả hướng tăng nhanh nhất của loss_value = f(W) xung quanh W0, cũng như độ dốc của sự tăng này. Mỗi đạo hàm riêng biệt mô tả độ dốc của f theo một hướng cụ thể. Vì lý do này, tương tự như với một hàm f(x), ta có thể giảm giá trị của f(x) bằng cách di chuyển x một chút theo hướng ngược lại với đạo hàm, với một hàm f(W) của một tensor, ta có thể giảm loss_value = f(W) bằng cách di chuyển W theo hướng ngược lại với độ dốc: ví dụ, W1 = W0 – step * grad(f(W0), W0) (ở đây step là một hệ số tỷ lệ nhỏ). Điều này có nghĩa là đi ngược lại hướng tăng nhanh nhất của f.
Stochastic Gradient Descent (SGD)
Cho một hàm có thể đạo hàm, giá trị nhỏ nhất của một hàm là một điểm mà đạo hàm bằng 0, vì vậy ta chỉ cần tìm tất cả các điểm mà đạo hàm bằng 0 và kiểm tra xem ở những điểm này hàm có giá trị nhỏ nhất hay không.
Áp dụng vào mạng neural, điều này có nghĩa là tìm ra một cách phân tích kết hợp giá trị trọng số sao cho hàm mất mát có giá trị nhỏ nhất có thể. Điều này có thể thực hiện bằng cách giải phương trình grad(f(W), W) = 0 cho W. Đây là một phương trình đa thức của N biến, trong đó N là số hệ số trong mô hình. Mặc dù có thể giải phương trình này cho N = 2 hoặc N = 3, nhưng làm như vậy là không khả thi đối với các mạng neural thực tế – số lượng tham số không bao giờ ít hơn vài nghìn và thường có thể là vài chục triệu.
Thay vào đó, ta có thể sử dụng thuật toán:
- Rút ra một lô mẫu huấn luyện, x, và các mục tiêu tương ứng, y_true.
- Chạy mô hình trên x để có dự đoán, y_pred (đây được gọi là bước chuyển tiếp – forwarding).
- Tính toán mất mát của mô hình trên lô dữ liệu, một giá trị đo lường sự không phù hợp giữa y_pred và y_true.
- Tính toán đạo hàm của mất mát đối với các tham số của mô hình (đây được gọi là bước lùi – backward pass).
- Di chuyển các tham số một chút theo hướng ngược lại từ đạo hàm – ví dụ, W = W – learning_rate * gradient – từ đó giảm mất mát trên lô một chút. Tốc độ học (ở đây là learning_rate) sẽ là một hệ số vô hướng điều chỉnh “tốc độ” của quá trình gradient descent.
Dễ hiểu, đó chính là phương pháp mini-batch stochastic gradient descent (mini-batch SGD) mà mình vừa mô tả. Thuật ngữ “stochastic” liên quan đến việc mỗi lô dữ liệu được rút ra một cách ngẫu nhiên (stochastic là một từ đồng nghĩa với random). Hình bên dưới mô tả những gì xảy ra trong không gian 1D, khi mô hình chỉ có một tham số và ta chỉ có 1 mẫu huấn luyện.
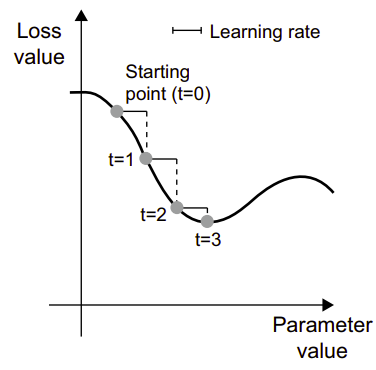
Như các bạn có thể thấy, một cách hiệu quả là chọn một giá trị hợp lý cho hệ số learning_rate. Nếu nó quá nhỏ, quá trình đi xuống theo đường cong sẽ mất nhiều vòng lặp, và có thể bị kẹt trong một cực tiểu nào đó. Nếu learning_rate quá lớn, các bước cập nhật có thể dẫn tới các vị trí hoàn toàn ngẫu nhiên trên đường cong.
Lưu ý rằng một biến thể của thuật toán mini-batch SGD là vẽ một mẫu và mục tiêu duy nhất ở mỗi vòng lặp, thay vì vẽ một lô dữ liệu. Điều này sẽ là true SGD (khác với mini-batch SGD). Ngược lại, ta cũng có thể chạy mọi bước trên toàn bộ dữ liệu có sẵn, đó là batch gradient descent. Mỗi cập nhật sẽ chính xác hơn, nhưng tốn kém hơn.
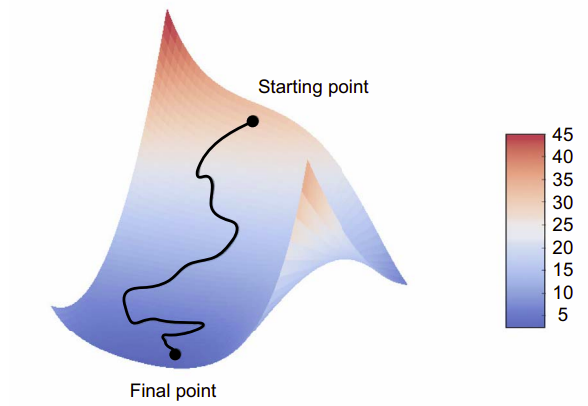
Trong thực tế, ta sẽ sử dụng gradient descent trong các không gian có chiều cao: mỗi hệ số trọng số trong mạng neural là một chiều tự do trong không gian, và có thể có hàng chục nghìn hoặc thậm chí hàng triệu chiều. Ví dụ hình trên là trong không gian 2D.
Hình bên dưới thể hiện đường cong mất mát như một hàm của một tham số mô hình.
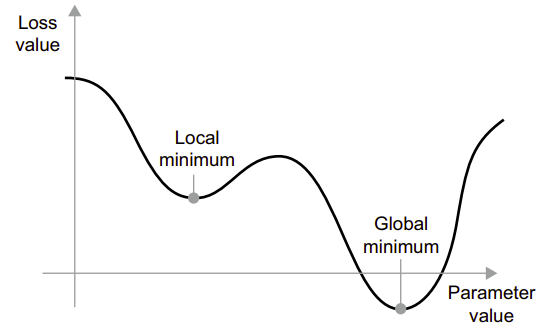
Như hình trên, xung quanh một giá trị tham số cụ thể, có một điểm cực tiểu cục bộ: xung quanh điểm đó, di chuyển sang trái sẽ dẫn đến sự tăng mất mát, nhưng cũng vậy nếu di chuyển sang phải.
Nếu tham số đang được tối ưu hóa thông qua SGD với một learning rate nhỏ, quá trình tối ưu hóa có thể bị kẹt tại điểm cực tiểu cục bộ thay vì đến điểm cực tiểu toàn cầu. Ta có thể tránh những vấn đề như vậy bằng cách sử dụng đà (momentum), lấy cảm hứng từ lĩnh vực vật lý. Tưởng tượng quá trình tối ưu hóa như một quả bóng nhỏ lăn xuống đường cong mất mát. Nếu nó có đủ đà, quả bóng sẽ không bị kẹt ở một “thung lũng” và sẽ đến được điểm cực tiểu toàn cầu. Đà được thực hiện bằng cách di chuyển quả bóng ở mỗi bước dựa không chỉ vào giá trị độ dốc hiện tại (gia tốc hiện tại) mà còn vào vận tốc hiện tại (kết quả từ gia tốc trước đó). Trong thực tế, điều này có nghĩa là cập nhật tham số w không chỉ dựa trên giá trị độ dốc hiện tại mà còn dựa trên cập nhật tham số trước đó.
past_velocity = 0.
momentum = 0.1
while loss > 0.01:
w, loss, gradient = get_current_parameters()
velocity = past_velocity * momentum - learning_rate * gradient
w = w + momentum * velocity - learning_rate * gradient
past_velocity = velocity
update_parameter(w)







Comments 2