Tiếp nối phần Lý thuyết toán cơ bản trong Deep Learning, bài viết này sẽ trình bày tiếp về các phép toán trên tensor cũng như diễn giải hình học.
Tất cả các biến đổi mà mạng nơ-ron sâu học được có thể được giảm xuống thành các phép toán tensor (hoặc hàm tensor) được áp dụng cho các tensor chứa dữ liệu số.
keras.layers.Dense(512, activation="relu")Layer này có thể được hiểu như là một hàm, nhận một ma trận làm đầu vào và trả về một ma trận khác – một biểu diễn mới cho tensor đầu vào. Cụ thể, hàm có dạng như sau (trong đó W là một ma trận và b là một vector, đều là thuộc tính của layer).
output = relu(dot(input, W) + b)
Chúng ta có ba phép toán tensor ở đây:
- Một tích vô hướng (dot) giữa tensor đầu vào và một tensor có tên là W.
- Một phép cộng (+) giữa ma trận kết quả và một vector b.
- Một phép relu:
relu(x)làmax(x, 0); “relu” là viết tắt của “rectified linear unit” (đơn vị tuyến tính được điều chỉnh).
Các phép toán theo phần tử
Phép toán relu và phép cộng là các phép toán theo phần tử (element-wise operations). Các phép toán được áp dụng độc lập cho mỗi phần tử trong các tensor đang xem xét. Điều này có nghĩa là những phép toán này rất thích hợp cho các triển khai đồng thời (triển khai vector hóa – một thuật ngữ xuất phát từ kiến trúc siêu máy tính xử lý vector từ thập kỷ 1970-90). Đối với relu:
def naive_relu(x):
assert len(x.shape) == 2
x = x.copy()
for i in range(x.shape[0]):
for j in range(x.shape[1]):
x[i, j] = max(x[i, j], 0)
return xĐối với phép cộng:
def naive_add(x, y):
assert len(x.shape) == 2
assert x.shape == y.shape
x = x.copy()
for i in range(x.shape[0]):
for j in range(x.shape[1]):
x[i, j] += y[i, j]
return xTrên cùng nguyên tắc đó, ta có thể thực hiện phép nhân theo phần tử, phép trừ, và cũng như vậy.
import numpy as np
z = x + y
z = np.maximum(z, 0.)Broadcasting
Hàm naive_add phía trên chỉ hỗ trợ phép cộng giữa các tensor có hạng là 2 và có shape giống nhau. Nhưng trong class Dense đã giới thiệu trước đó (ở đoạn code đầu tiên bài viết này), ta đã thêm một tensor hạng 2 với một vector. Điều gì sẽ xảy ra khi shape của hai tensor khác nhau và được cộng với nhau? Đó là tensor nhỏ hơn sẽ được broadcast để phù hợp với shape của tensor lớn hơn. Quá trình broadcast bao gồm 2 bước:
- Các trục (được gọi là trục broadcast được thêm vào tensor nhỏ hơn để phù hợp với ndim của tensor lớn hơn.
- Tensor nhỏ hơn được lặp lại theo các trục mới này để phù hợp với shape đầy đủ của tensor lớn hơn.
Giả sử có tensor X với shape là (32, 10) và tensor y với shape là (10,).
import numpy as np
X = np.random.random((32, 10))
y = np.random.random((10,))Trước hết, ta thêm một trục đầu tiên trống vào tensor y, khiến cho shape của nó trở thành (1, 10):
y = np.expand_dims(y, axis=0)Sau đó, ta lặp lại tensor y 32 lần theo chiều của trục mới này, để cuối cùng chúng ta thu được tensor Y với shape là (32, 10), trong đó Y[i, :] == y cho i trong khoảng từ 0 đến 32:
Y = np.concatenate([y] * 32, axis=0)Ở điểm này, ta có thể tiếp tục thực hiện phép cộng giữa X và Y, vì chúng có cùng shape. Về mặt triển khai, không có tensor mới hạng 2 được tạo ra, vì điều đó sẽ rất không hiệu quả.
def naive_add_matrix_and_vector(x, y):
assert len(x.shape) == 2
assert len(y.shape) == 1
assert x.shape[1] == y.shape[0]
x = x.copy()
for i in range(x.shape[0]):
for j in range(x.shape[1]):
x[i, j] += y[j]
return xVới phép broadcasting, ta thường có thể thực hiện các phép toán theo từng phần tử trên hai tensor đầu vào nếu một tensor có shape là (a, b, … n, n + 1, … m) và tensor kia có shape là (n, n + 1, … m). Phép broadcast sẽ tự động xảy ra cho các trục từ a đến n – 1. Dưới đây là một ví dụ sử dụng phép toán tối đa theo từng phần tử giữa hai tensor có hình dạng khác nhau thông qua phép broadcast:
import numpy as np
x = np.random.random((64, 3, 32, 10))
y = np.random.random((32, 10))
z = np.maximum(x, y)Phép nhân tensor
Phép nhân tensor, hay còn gọi là phép nhân chấm (không nên nhầm lẫn với phép nhân theo từng phần tử, toán tử *), là một trong những phép toán tensor phổ biến và hữu ích nhất. Trong NumPy, phép nhân tensor được thực hiện bằng cách sử dụng hàm np.dot (vì ký hiệu toán học cho phép nhân tensor thường là dấu chấm):
x = np.random.random((32,))
y = np.random.random((32,))
z = np.dot(x, y)Trong ký hiệu toán học, phép toán này được kí hiệu bằng dấu chấm (•).
Vậy phép toán dot hoạt động như thế nào? Hãy bắt đầu với tích vô hướng của hai vector, x và y. Nó được tính như sau:
def naive_vector_dot(x, y):
assert len(x.shape) == 1
assert len(y.shape) == 1
assert x.shape[0] == y.shape[0]
z = 0.
for i in range(x.shape[0]):
z += x[i] * y[i]
return zTa thấy rằng tích vô hướng giữa hai vector là một scalar và chỉ có các vector có cùng số lượng phần tử mới phù hợp cho phép toán dot. Ta cũng có thể thực hiện phép toán dot giữa một ma trận x và một vector y, kết quả trả về một vector trong đó các hệ số là tích vô hướng giữa y và các hàng của x. Ta có thể triển khai nó như sau.
def naive_matrix_vector_dot(x, y):
assert len(x.shape) == 2
assert len(y.shape) == 1
assert x.shape[1] == y.shape[0]
z = np.zeros(x.shape[0])
for i in range(x.shape[0]):
for j in range(x.shape[1]):
z[i] += x[i, j] * y[j]
return zNgắn gọn:
def naive_matrix_vector_dot(x, y):
z = np.zeros(x.shape[0])
for i in range(x.shape[0]):
z[i] = naive_vector_dot(x[i, :], y)
return zLưu ý khi một trong hai tensor có ndim lớn hơn 1, phép toán dot không còn là đối xứng, có nghĩa là dot(x, y) không giống như dot(y, x).
Tất nhiên, phép nhân dot có thể tổng quát hóa cho các tensor có một số lượng trục tùy ý. Ứng dụng phổ biến nhất có thể là phép nhân dot giữa hai ma trận. Ta có thể thực hiện phép nhân dot giữa hai ma trận x và y (dot(x, y)) nếu và chỉ nếu x.shape[1] == y.shape[0]. Kết quả là một ma trận có hình dạng (x.shape[0], y.shape[1]), trong đó các hệ số là tích vô hướng giữa các hàng của x và các cột của y.
def naive_matrix_dot(x, y):
assert len(x.shape) == 2
assert len(y.shape) == 2
assert x.shape[1] == y.shape[0]
z = np.zeros((x.shape[0], y.shape[1]))
for i in range(x.shape[0]):
for j in range(y.shape[1]):
row_x = x[i, :]
column_y = y[:, j]
z[i, j] = naive_vector_dot(row_x, column_y)
return zXem hình dưới để hiểu rõ hơn:
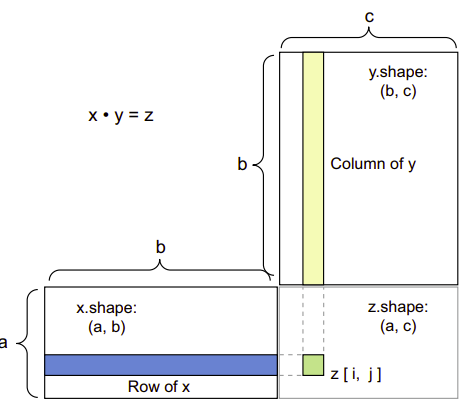
Nói chung, ta có thể thực hiện phép nhân dot giữa các tensor có số chiều cao hơn, theo các quy tắc tương thích hình dạng giống như đã được mô tả trước đó cho trường hợp 2D.
(a, b, c, d) • (d,) → (a, b, c)
(a, b, c, d) • (d, e) → (a, b, c, e)Tensor reshape
Một loại phép toán tensor thứ ba quan trọng để hiểu là thay đổi hình dạng tensor (tensor reshape).
train_images = train_images.reshape((60000, 28 * 28))Thay đổi hình dạng của một tensor có nghĩa là sắp xếp lại các hàng và cột của nó để phù hợp với một hình dạng mục tiêu. Đương nhiên, tensor đã thay đổi shape sẽ có cùng số lượng hệ số tổng cộng như tensor ban đầu. Việc thay đổi hình dạng được hiểu rõ nhất thông qua ví dụ đơn giản sau:
>>> x = np.array([[0., 1.],
[2., 3.],
[4., 5.]])
>>> x.shape
(3, 2)
>>> x = x.reshape((6, 1))
>>> x
array([[ 0.],
[ 1.],
[ 2.],
[ 3.],
[ 4.],
[ 5.]])
>>> x = x.reshape((2, 3))
>>> x
array([[ 0., 1., 2.],
[ 3., 4., 5.]])Một trường hợp đặc biệt của thay đổi hình dạng mà thường gặp là phép chuyển vị. Chuyển vị một ma trận có nghĩa là hoán đổi các hàng và cột của nó, sao cho x[i, :] trở thành x[:, i].
>>> x = np.zeros((300, 20))
>>> x = np.transpose(x)
>>> x.shape
(20, 300)Diễn giải hình học về các phép toán tensor trong Deep Learning
Phép toán tensor có thể được hiểu theo góc độ hình học bởi vì nội dung của các tensor được thao tác có thể được hiểu như là tọa độ của các điểm trong không gian hình học nào đó. Do đó, tất cả các phép toán tensor đều có một diễn giải hình học. Chẳng hạn phép cộng:
A = [0.5, 1]Đó là một điểm trong không gian 2 chiều.
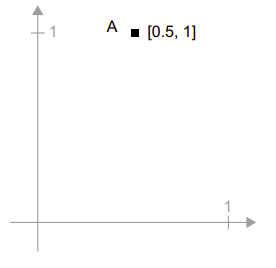
Một vector được thể hiện như một mũi tên nối từ gốc tọa độ đến điểm đó như hình bên dưới.
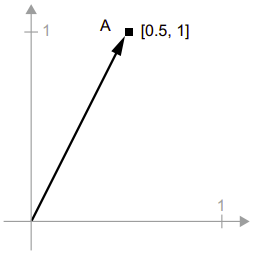
Cho điểm B = [1, 0.25] vector AB được biểu diễn bằng hình học bằng cách nối các mũi tên vector lại với nhau, với vị trí kết quả là vector đại diện cho tổng của hai vector trước đó.
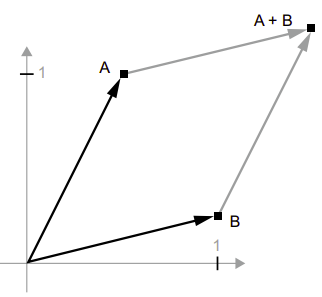
Như các bạn có thể thấy, việc cộng vector B vào vector A đại diện cho việc sao chép điểm A vào một vị trí mới, với khoảng cách và hướng từ điểm ban đầu A được xác định bởi vector B. Nếu ta áp dụng phép cộng vector tương tự cho một nhóm điểm trong mặt phẳng (một “đối tượng”), ta sẽ tạo ra một bản sao của toàn bộ đối tượng ở một vị trí mới.
Do đó, phép cộng tensor đại diện cho hành động dịch chuyển một đối tượng (di chuyển đối tượng mà không làm biến dạng nó) một lượng nhất định theo một hướng cụ thể.
Nói chung, các phép toán hình học cơ bản như dịch chuyển (translation), xoay (rotating), co giãn (scaling), nghiêng (skewing), và những phép toán khác có thể được biểu diễn dưới dạng các phép toán tensor. Dưới đây là một số ví dụ:
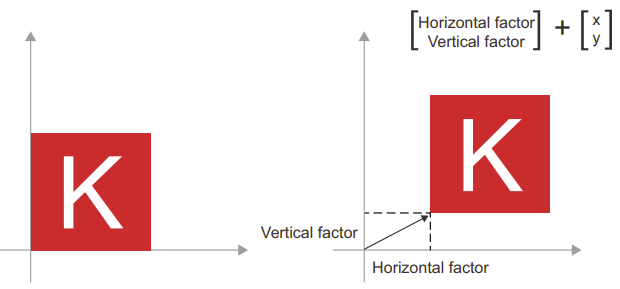
- Dịch chuyển (Translation): Việc cộng một vector vào một điểm sẽ di chuyển điểm đó một lượng cố định theo một hướng cố định. Khi áp dụng cho một tập hợp điểm (như một đối tượng 2D), điều này được gọi là “dịch chuyển“.
- Xoay (Rotation): Xoay ngược chiều kim đồng hồ của một vector 2D một góc theta (như hình bên dưới) có thể được thực hiện thông qua tích vô hướng với ma trận 2 × 2 là R = [[cos(theta), -sin(theta)], [sin(theta), cos(theta)]].
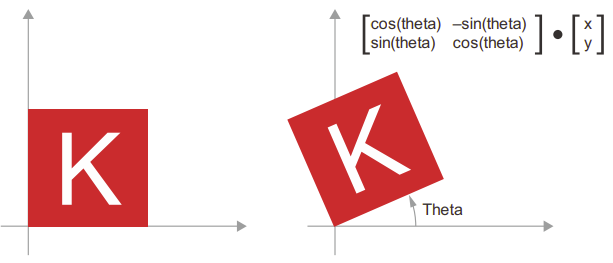
- Co giãn (Scaling): Co giãn theo chiều dọc và chiều ngang của hình ảnh có thể được thực hiện thông qua tích vô hướng với ma trận 2 × 2 là S = [[horizontal_factor, 0], [0, vertical_factor]] (lưu ý rằng ma trận như vậy được gọi là “ma trận chéo,” vì nó chỉ có các hệ số khác 0 trên “đường chéo” của nó, từ trên cùng bên trái đến dưới cùng bên phải).
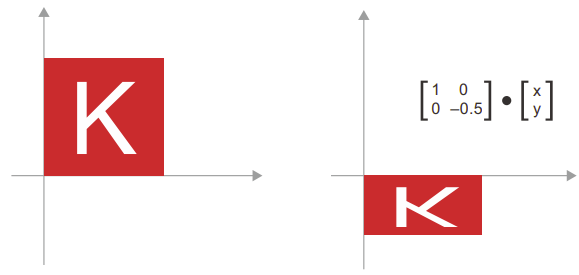
- Biến đổi tuyến tính (Linear transform): Tích vô hướng với một ma trận tùy ý thực hiện một biến đổi tuyến tính. Lưu ý rằng phép co giãn và phép xoay theo định nghĩa là biến đổi tuyến tính.
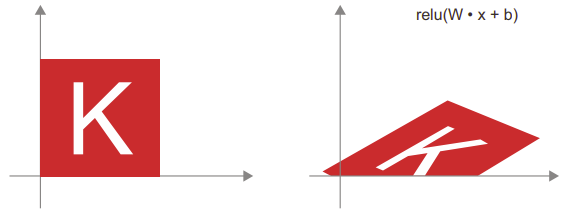
- Biến đổi affine: Một biến đổi affine (hình dưới) là sự kết hợp giữa một biến đổi tuyến tính (thực hiện thông qua tích vô hướng với một số ma trận) và một dịch chuyển (thực hiện thông qua việc cộng thêm một vector). Đó chính xác là phép tính y = W • x + b được thực hiện bởi lớp Dense! Một lớp Dense mà không có hàm kích hoạt là một lớp affine.
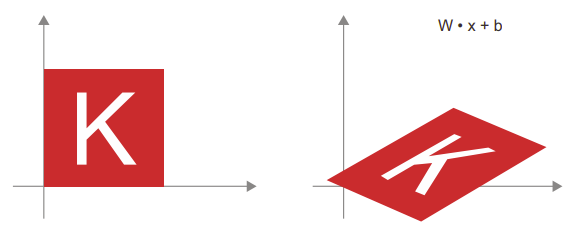
- Layer Dense với hàm kích hoạt relu: Một quan sát quan trọng về các biến đổi affine là nếu ta áp dụng chúng nhiều lần liên tiếp, ta vẫn sẽ thu được một biến đổi affine (vì vậy ta có thể áp dụng một biến đổi affine đó từ đầu). Thử với hai lớp:
affine2(affine1(x)) = W2 • (W1 • x + b1) + b2 = (W2 • W1) • x + (W2 • b1 + b2). Đó là một biến đổi affine với phần tuyến tính là ma trận W2 • W1 và phần dịch chuyển là vector W2 • b1 + b2. Do đó, một mạng nơ-ron nhiều lớp được tạo hoàn toàn từ các lớp Dense mà không có hàm kích hoạt sẽ tương đương với một lớp Dense duy nhất. Mạng nơ-ron “sâu” này chỉ là một mô hình tuyến tính ẩn! Đây là lý do tại sao ta cần các hàm kích hoạt, như relu. Nhờ các hàm kích hoạt, một chuỗi các lớp Dense có thể được thiết kế để thực hiện các biến đổi hình học phi tuyến, tạo ra không gian giả định rất phong phú cho các mạng nơ-ron sâu.









Comments 1