Trong thuật toán trước đó, chúng ta đã giả định có thể dễ dàng tính đạo hàm của một hàm số. Nhưng liệu điều đó có đúng với mọi trường hợp không? Làm thế nào chúng ta có thể tính đạo hàm của các biểu thức phức tạp trong thực tế? Đó là cảm hứng cho thuật toán Lan truyền ngược (Backpropagation) xuất hiện.
Lan truyền ngược là một phương pháp sử dụng đạo hàm của các phép toán đơn giản (như cộng, relu, hoặc tích tensor) để dễ dàng tính đạo hàm của sự kết hợp phức tạp bất kỳ của những phép toán nguyên tử này. Quan trọng là một mạng neural bao gồm nhiều phép toán tensor được kết hợp lại, mỗi phép toán này có đạo hàm đơn giản và đã biết trước. Ví dụ, mô hình có thể được biểu diễn dưới dạng một hàm được tham số hóa bởi các biến W1, b1, W2 và b2 (thuộc về lần lượt lớp Dense thứ nhất và thứ hai), liên quan đến các phép toán nguyên tử như dot, relu, softmax và +, cũng như hàm mất mát, đều có thể tính đạo hàm một cách dễ dàng.
loss_value = loss(y_true, softmax(dot(relu(dot(inputs, W1) + b1), W2) + b2))Một chuỗi các hàm như vậy có thể được suy ra bằng cách sử dụng công thức sau đây, gọi là quy tắc chuỗi (chain rule). Xét hai hàm f và g, cũng như hàm tổ hợp fg sao cho fg(x) == f(g(x)):
def fg(x):
x1 = g(x)
y = f(x1)
return ySau đó, quy tắc chuỗi (chain rule) khẳng định rằng grad(y, x) == grad(y, x1) * grad(x1, x). Điều này cho phép ta tính đạo hàm của hàm tổ hợp fg miễn rằng biết được đạo hàm của f và g. Quy tắc chuỗi được đặt tên như vậy vì khi thêm vào nhiều hàm trung gian hơn, nó bắt đầu trông giống như một chuỗi:
def fghj(x):
x1 = j(x)
x2 = h(x1)
x3 = g(x2)
y = f(x3)
return y
grad(y, x) == (grad(y, x3) * grad(x3, x2) * grad(x2, x1) * grad(x1, x))Áp dụng quy tắc chuỗi vào việc tính toán các giá trị đạo hàm của mạng neural dẫn đến một thuật toán được gọi là lan truyền ngược (backpropagation).
Tự động khác biệt với đồ thị tính toán
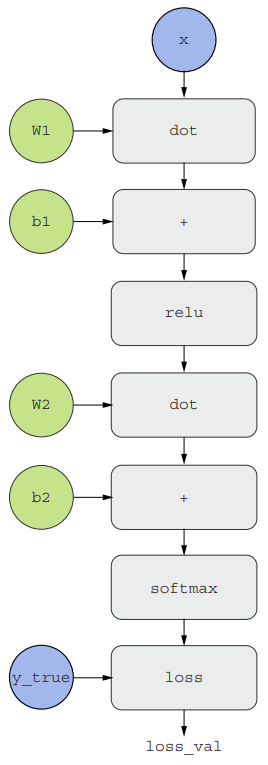
Một cách hữu ích để hiểu về backpropagation là qua khái niệm về đồ thị tính toán (computation graphs). Một đồ thị tính toán là cấu trúc dữ liệu nằm ở trung tâm của TensorFlow và mạng học sâu nói chung. Đó là một đồ thị có hướng không chu trình của các phép toán – trong trường hợp này là các phép toán tensor. Ví dụ, hình trên thể hiện biểu diễn đồ thị của mô hình đầu tiên của chúng ta. Đồ thị tính toán đã trở thành một khái niệm rất thành công trong ngành khoa học máy tính vì chúng cho phép xử lý tính toán như dữ liệu: một biểu thức có thể tính toán được được mã hóa thành một cấu trúc dữ liệu có thể đọc được bởi máy, có thể được sử dụng làm đầu vào hoặc đầu ra của một chương trình khác. Ví dụ có một chương trình nhận vào một đồ thị tính toán và có thể tự động tạo ra đạo hàm của biểu thức đó. Điều này dễ dàng hơn nếu tính toán đó được biểu diễn dưới dạng một cấu trúc dữ liệu đồ thị rõ ràng chẳng hạn như file .py.
Xét một ví dụ cơ bản về đồ thị tính toán như hình dưới. Trong đó ta chỉ có một lớp tuyến tính và tất cả các biến là scalar. Ta sẽ sử dụng hai biến scalar w và b, một đầu vào scalar x, và áp dụng một số phép toán để kết hợp chúng thành một đầu ra y. Cuối cùng, ta sẽ áp dụng một hàm mất mát giá trị tuyệt đối: loss_val = abs(y_true - y). Vì chúng ta muốn cập nhật w và b sao cho giảm thiểu loss_val, ta sẽ quan tâm đến việc tính grad(loss_val, b) và grad(loss_val, w).
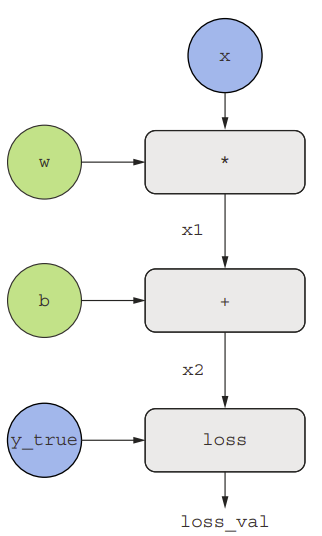
Ta có đầu vào x, mục tiêu y_true, w, và b. Chúng ta sẽ truyền giá trị này đến tất cả các nút trong đồ thị, từ trên xuống dưới, cho đến khi chúng ta đạt được loss_val. Đây là quá trình chuyển tiếp (forwarding).
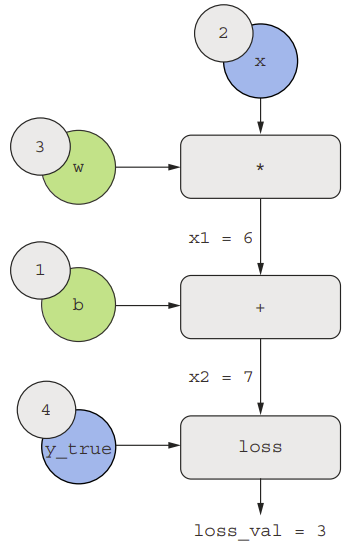
Bây giờ hãy “đảo ngược” đồ thị: đối với mỗi cạnh trong đồ thị đi từ A đến B, ta sẽ tạo một cạnh ngược lại từ B đến A và hỏi, B thay đổi bao nhiêu khi A thay đổi? Nói cách khác, grad(B, A) là bao nhiêu?
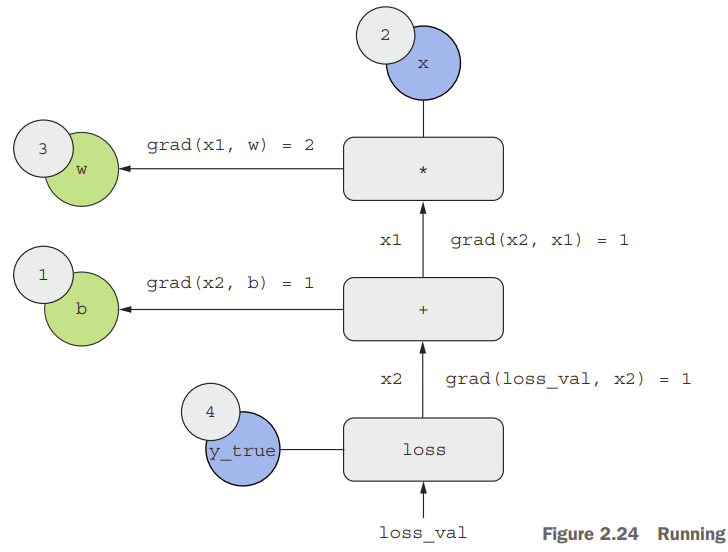
Chúng ta có những giá trị sau đây:
- grad(
loss_val,x2) = 1, vì khix2thay đổi một lượng epsilon,loss_val= abs(4 –x2) cũng thay đổi một lượng tương đương. - grad(
x2,x1) = 1, vì khix1thay đổi một lượng epsilon,x2=x1+b=x1+ 1 cũng thay đổi một lượng tương đương. - grad(
x2,b) = 1, vì khibthay đổi một lượng epsilon,x2=x1+b= 6 +bcũng thay đổi một lượng tương đương. - grad(
x1,w) = 2, vì khiwthay đổi một lượng epsilon,x1=x*w= 2 *wthay đổi bởi 2 * epsilon.
Ta hoàn toàn có thể thu được đạo hàm của một nút đối với một nút khác bằng cách nhân các đạo hàm cho mỗi cạnh theo cạnh nối giữa 2 node. Ví dụ, grad(loss_val, w) = grad(loss_val, x2) * grad(x2, x1) * grad(x1, w).
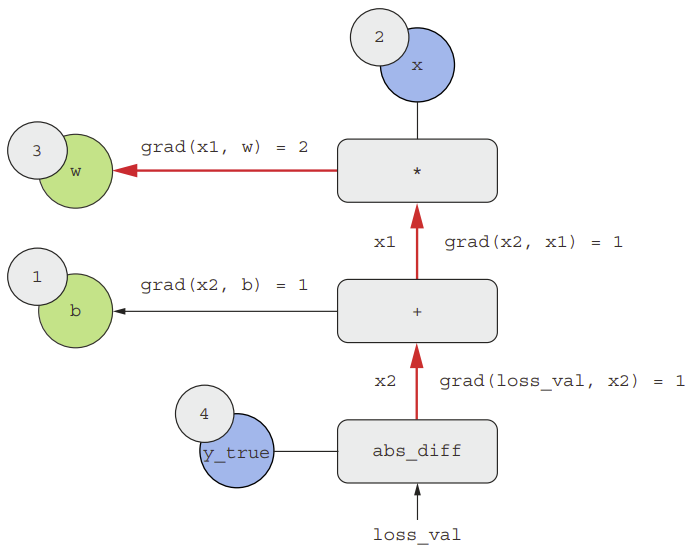
Bằng cách áp dụng quy tắc chuỗi, ta thu được:
- grad(
loss_val,w) = 1 * 1 * 2 = 2 - grad(
loss_val,b) = 1 * 1 = 1
Lưu ý, nếu có nhiều đường dẫn nối hai nút quan tâm, a và b, trong đồ thị đảo ngược, ta sẽ thu được grad(b, a) bằng cách tổng hợp đóng góp của tất cả các đường dẫn.
Gradient trong Tensorflow – Thuật toán lan truyền ngược
API GradientTape hỗ trợ chúng ta tận dụng khả năng khác biệt tự động mạnh mẽ của TensorFlow. Đó là một phạm vi Python sẽ “ghi lại” các phép toán tensor chạy bên trong nó, dưới dạng một đồ thị tính toán (đôi khi được gọi là “băng ghi” – tape). Đồ thị này sau đó có thể được sử dụng để lấy lại độ dốc của bất kỳ đầu ra nào đối với bất kỳ biến số nào hoặc tập hợp các biến số (là các instance của class tf.Variable). Một tf.Variable là một loại tensor cụ thể được thiết kế để giữ trạng thái có thể thay đổi, ví dụ như trọng số của một mạng nơ-ron luôn là các instance của tf.Variable.
import tensorflow as tf
x = tf.Variable(0.)
with tf.GradientTape() as tape:
y = 2 * x + 3
grad_of_y_wrt_x = tape.gradient(y, x)GradientTape hoạt động với các phép toán tensor:
x = tf.Variable(tf.random.uniform((2, 2)))
with tf.GradientTape() as tape:
y = 2 * x + 3
grad_of_y_wrt_x = tape.gradient(y, x)Nó cũng hoạt động với danh sách các biến số:
W = tf.Variable(tf.random.uniform((2, 2)))
b = tf.Variable(tf.zeros((2,)))
x = tf.random.uniform((2, 2))
with tf.GradientTape() as tape:
y = tf.matmul(x, W) + b
grad_of_y_wrt_W_and_b = tape.gradient(y, [W, b])




![[CEH] Module 7 - Phần 6: Tìm hiểu về fileless malware 15 [CEH] Module 7 – Phần 6: Tìm hiểu về fileless malware](https://sinhviencntt.net/wp-content/uploads/2024/03/m7-p6-75x75.png)